

Article of the Month - September 2017 |
Correction of Terrestrial LiDAR Data Using a Hybrid ModelWallace MUKUPA, China, Gethin Wyn ROBERTS, United Kingdom, Craig Matthew HANCOCK, China, Khalil AL-MANASIR, China
Wallace Mukupa
This article in .pdf-format (27 pages) 1) This paper is a peer review paper that was presented at the FIG Working Week 2017. Wallace Mukupa received a ph.d. grant from FIG Foundation in 2016 and one of the results is this peer review paper. In this paper, a hybrid method for correcting intensity data is presented. Read Wallace Mukupa's report about the Ph.D. grant and from the FIG Working Week SUMMARYThe utilization of Terrestrial Laser Scanning (TLS) intensity data in the field of surveying engineering and many other disciplines is on the increase due to its wide applicability in studies such as change detection, deformation monitoring and material classification. Radiometric correction of TLS data is an important step in data processing so as to reduce the error in the data. In this paper, a hybrid method for correcting intensity data has been presented. The proposed hybrid method aims at addressing two issues. Firstly, the issue of near distance effects for scanning measurements that are taken at short distances (1 to 6 metres) and secondly, it takes into account the issue of target surface roughness as expounded in the Oren-Nayar reflectance model. The proposed hybrid method has been applied to correct concrete intensity data that was acquired using the Leica HDS7000 laser scanner. The results of this proposed correction model are presented to demonstrate its feasibility and validity. 1. INTRODUCTIONCorrection of intensity data is essential due to systematic effects in the LiDAR system parameters and measurements and in order to ensure the best accuracy of the delivered products (Habib et al., 2011). The whole aim of radiometric correction is to convert the laser returned intensity recorded by the laser scanner to a value that is proportional to the object reflectance (Antilla et al., 2011). This correction of intensity data is still an open area of investigation and this is the case because even though a couple of researchers have studied the subject of TLS intensity correction for instance, a standard correction method that can be applicable for all the various types of laser scanners is non-existent (Penasa et al., 2014). Such a scenario is also explained by some of the laser scanning research work that are still being published without the intensity data having been corrected (Krooks et al., 2013). However, in Tan and Cheng (2015), it is purported that the proposed intensity correction method is suitable for all TLS instruments. In the case of Airborne Laser Scanning (ALS), the subject of intensity data correction has an old history compared to TLS and this has been reported by researchers such as Kaasalainen et al. (2011). It has been reported that the effect of the measurement range (distance) on the intensity data depends on several parameters. In the case of TLS, the effects of the range tend to depend on the instrument especially when measurements are taken at close range to the target. The effects of the range on TLS intensity or the dependence of the received power as a function of the range is proportional to 1/R2 (R = range) in the case of extended diffuse targets (Jelalian, 1992). This implies that the whole laser footprint is reflected on one surface and it has Lambertian scattering properties. However, non-extended diffuse targets exhibit different range dependencies. For instance, point targets (e.g. a leaf) with an area smaller than the footprint are range independent and targets with linear physical properties (e.g. wire) are linear range dependent. Therefore, the range dependency becomes 1/R4 for targets smaller than laser footprint size and 1/R3 for linear targets (Vain and Kaasalainen, 2011). According to Krooks et al. (2013), different scanners have different instrumental effects on the measured intensity and this implies that it is prudent to study each scanner individually. Instrumental effects have been reported to affect the intensity recorded for TLS instruments. Even though distance has been predicted to follow the range squared inverse (1/R2) dependency for extended targets based on the physical model (radar equation), in practical applications this prediction is inapplicable at all ranges because of TLS instrumental modifications that are designed to enhance the range measurement determination (Holfe and Pfeifer, 2007; Balduzzi et al., 2011; Antilla et al., 2011). In a similar vein, Kaasalainen et al. (2011) state that the knowledge of the TLS instrument as to whether it has near-distance reducers or logarithmic amplifiers in the case of small reflectance is of cardinal importance in an attempt to know the distance effects and the extent to which the measured intensity is affected by instrumental effects. In Kaasalainen et al. (2009a) it is has been reported that measurement of the intensity taken at short ranges, 1m in this case have been significantly affected at such near distances by brightness reducers. The effects of the incidence angle on the intensity are related to the scanned target object in terms of its surface structure and scattering properties (Krooks et al., 2013). In terms of the rugosity of the target, macroscopic irregularities of the order of mm to cm size and almost the same size as the laser footprint, neutralize the effects of the incidence angle on the intensity. This is so because there are always elements on the surface of the target that are perpendicular to the incident laser beam (Kaasalainen et al., 2011). In a similar vein Penasa et al. (2014) states that the effects of the scattering angle can be neglected if the surface roughness of the target is comparable with the laser spot size. Other studies for instance Kaasalainen et al. (2009b) showed that the significance of the angle of incidence only becomes an important parameters when it is greater than 20° for several materials. The strength of the signal that the scanner receives is dependent on the backscattering properties of the target scanned (Shan and Toth, 2009). If the surface backscattering the laser is an extended target and a Lambertian reflector, the backscatter strength in the angular domain depends entirely on the incidence angle. Different TLS intensity correction models have been proposed and some methods are based on the physical model (laser range equation) whereas others are modified versions of the physical model and some are data driven. For instance in Balduzzi et al. (2011) the modified radar range equation was used to correct the intensity data. It is reported that the laser scanner (FARO LS880) which was used has an intensity filter and with the assumption that this filter has only an impact on the intensity variations due to distance, the range squared inverse law was replaced by a device specific distance function and then a logarithmic function was applied. In Kaasalainen et al. (2008), an important consideration was the effect of the logarithmic amplifier of the FARO LS HE80 for small reflectance. The logarithmic correction was calibrated by fitting an exponential function. In Penasa et al. (2014) an intensity correction approach for distance effects and exclusive of other variables such as incidence angle or atmospheric losses is presented. The correction approach did not apply the radar equation instead it is stated that the correction was based on estimating a correcting intensity-distance function on an appropriate reference point cloud via a Nadaraya–Watson regression estimator. In Blaskow and Schneider (2014) an intensity correction approach is presented which involves polynomial approximation and static correction model. Under the polynomial approximation, the intensity-distance curves were functionalised as basis for the static correction model and the Spectralon target data served as reference. Pfeifer et al. (2007) investigated data driven models and a function, F(ρ, α, r) was sought to predict the intensity value from range (r), reflectivity (ρ) and incidence angle (α). To correct the intensity for the effects of target reflectivity and incidence angle, different functions were tested. The function which brought the curves to the closest overlap was (ρ cos(α))-0.16 and all intensity values were then multiplied by this function to remove the influence of target reflectivity and angle of incidence. Two linear functions were then fitted to correct the intensity for distance effects. In Franceschi et al. (2009) a study was undertaken that focused on using TLS intensity data to discriminate between marls and limestone, the corrected intensity was taken to be related and proportional to the target reflectivity and an assumption was made that the scanned objects were Lambertian reflectors. In Fang et al. (2015) an intensity correction method is presented based on estimating the laser transmission function so as to determine the ratio of the input laser signal between the limited and the unlimited ranges and then integrating this ratio in the radar range equation in order to correct the intensity data near distance effects. Tan and Cheng (2015) developed a model to correct the effects of the angle of incidence and the distance on the intensity data. The proposed correction model is approximated by a polynomial series based on the Weierstrass approximation theory and an approach to estimating the specific parameters is presented. Using a similar approach, Tan et al. (2016) proposed an intensity correction method for distance effects where the range squared inverse law as described in the radar equation and the ALS range correction methods was replaced by a polynomial function of distance. Zhu et al. (2015) investigated the use of TLS intensity data to detect leaf water content and an intensity correction method is described where firstly a reflection model was employed to get rid of specular reflection which was as a result of leaf surface at perpendicular angle and then reference targets were utilised to correct the effects of the angle of incidence. In view of the above, this study aimed at correcting the TLS returned intensity for concrete by looking at methods of modelling the variables that have an effect on the intensity values of the laser in this case the effects of the measurement range and incident angle since the experiment was carried out in a controlled environment. The focus of the investigation was to use existing models of laser behaviour to develop a correction model for TLS intensity data that is also capable of addressing near-distance effects and surface roughness of the target since not all objects are perfect Lambertian reflectors. The proposed hybrid intensity correction method is based on the radar equation (Jelalian, 1992), near-distance correction model (Fang et al., 2015) and the Oren-Nayar reflectance model (Carrea et al., 2016). These existing models and the development of a hybrid intensity correction model are explained in detail in the data processing section. A description of the experimental procedure for testing the proposed hybrid method for correcting intensity data is provided and the results of this correction model are presented to demonstrate the feasibility and validity of the method. 2. EXPERIMENTAL PROCEDURE2.1 Target Objects: Concrete SpecimensPrismatic concrete beams (Fig. 1) were used as scanning target objects mainly because this is part of an on-going project investigating the use of laser intensity for the assessment of fire-damaged concrete. Since surface roughness of the scanned object was of interest in this study, it is worth mentioning that the concrete consisted of fine aggregate (river sand) with a maximum grain size of 5 mm and crushed siliceous coarse aggregate with a diameter ranging from 5 to 20 mm. For easy identification, the concrete specimens were labelled as: Block C, Block 1, Block 2, Block 3 and Block 4.
Fig. 1: Concrete specimens 2.2 Scanning Room and EquipmentThe experiments were conducted under controlled laboratory conditions. The factors affecting the returned intensity under such conditions are the scanning geometry and the instrumental effects. Since the experiments were carried out in a controlled environment and at short range (1 to 6m), atmospheric losses were neglected. The Leica HDS7000 laser scanner (Fig. 2) was used to scan the concrete specimens and the technical specifications of this scanner are as presented in Table 1 below. Fig 2: HDS7000 Laser Scanner
Source: Leica Geosystems (2012) 2.3 Measurement Setup and Data AcquisitionThe measurement distances between the HDS7000 scanner and the target
objects (concrete specimens) were ranging from 1 to 6 metres and the
total station was utilized in marking out the scanning distances. The
steel frame where the blocks were placed was levelled using a spirit
level and then the distance to the prism placed right on the edge and
centre of the steel frame was measured. Distances up to 6m in steps of
1m were measured using a total station so as to have scans taken from
well-known accurate distances. The geometry of the experiment in terms
of scanning measurement setup is shown in Fig. 3. Fig. 3: Laser scanner and blocks at different levels on a frame (Letters A, B, C, D and E stand for shelf levels). With reference to Fig. 3, the planar surface of each concrete block was properly aligned with the frame edge with the aid of a mark which was made on the centre of the block and the frame too. These measures were carried out so as to position each concrete block at approximately the same required distance from the scanner for each respective scanning session. Independent measurements using a steel rule and tape were carried out to ensure that each concrete block was accurately oriented. The experiment was set-up this way in order to only focus on the scanning geometry which consists of the angle of incidence and the range between the scanner and the target object (Krooks et al., 2013; Kaasalainen et al., 2011) as the factor influencing the poor laser returned signal. The concrete blocks were placed at different heights on shelves of the steel frame with the control block on the centre shelf at the same height as the scanner with its front face approximately vertical and perpendicular to ensure that scanning was done at roughly normal angle of incidence. The scanning parameters used in the experiments involved super high resolution and a normal quality. 3. DATA PROCESSING 3.1 Scan Data Pre-processing The HDS7000 scans were converted to text files (.pts format) using the Z + F laser control software instead of the Leica Cyclone software as it has been reported for instance in Kaasalainen et al. (2011) that this software scales the intensity so as to accentuate visualisation. The scans which were converted to text files contained the geometric data in terms of X, Y and Z coordinates in a Cartesian coordinate system as well as radiometric data i.e. the intensity values for the 3D coordinates. The intensity values of data converted to text files were ranging from -2047 to +2048. The output Cartesian coordinates can be converted to spherical (range, zenith and azimuth angles) coordinates based on a zero origin for the TLS instrument as described in Eq. (1) (Soudarissanane et al., 2009):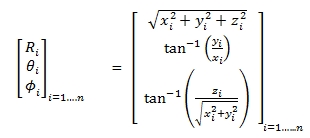 3.2 Intensity Data Correction
The proposed hybrid intensity correction method consists of two parts,
namely the near-distance correction model in Fang et al. (2015) and the
Oren-Nayar correction model described in Carrea et al. (2016). In
principle, the hybrid intensity correction method has a basis in the
radar (range) equation (Eq. (2)) and so an overview of this equation is
presented and then it is followed by the correction for near-distance
effects and the Oren-Nayar reflection model. The radar (range) equation
(Eq. (2)) consists of three main components and these are: the sensor,
the target and the environmental parameters which diminish the amount of
power transmitted. Importantly, this equation (Eq. (2)) has been applied
as a physical model for the correction of laser intensity data (Yan and
Shaker, 2014) in several studies where the equation has been applied
either as it is or in a modified form.
3.2 Intensity Data Correction
The proposed hybrid intensity correction method consists of two parts,
namely the near-distance correction model in Fang et al. (2015) and the
Oren-Nayar correction model described in Carrea et al. (2016). In
principle, the hybrid intensity correction method has a basis in the
radar (range) equation (Eq. (2)) and so an overview of this equation is
presented and then it is followed by the correction for near-distance
effects and the Oren-Nayar reflection model. The radar (range) equation
(Eq. (2)) consists of three main components and these are: the sensor,
the target and the environmental parameters which diminish the amount of
power transmitted. Importantly, this equation (Eq. (2)) has been applied
as a physical model for the correction of laser intensity data (Yan and
Shaker, 2014) in several studies where the equation has been applied
either as it is or in a modified form.
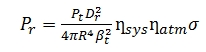 Where Pr is the received power, Pt is the power transmitted, Dr is the
receiver aperture, R is the range between the scanner and the target, βt
is the laser beam width, σ is the cross-section of the target, ηsys and
ηatm are system and atmospheric factors respectively. The cross-section
σ can be described as follows (Hӧfle and Pfeifer, 2007):
Where Pr is the received power, Pt is the power transmitted, Dr is the
receiver aperture, R is the range between the scanner and the target, βt
is the laser beam width, σ is the cross-section of the target, ηsys and
ηatm are system and atmospheric factors respectively. The cross-section
σ can be described as follows (Hӧfle and Pfeifer, 2007):
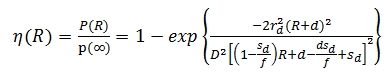 Where rd is the radius of the circular laser detector, d is the offset
between the measured range R and the object distance from the lens
plane, D is the diameter of the lens, Sd is the fixed distance of the
detector from the lens and f is the focal length. All of which are
parameters of the laser scanner. Combining Eq. (9) with Eq. (8) and
taking into account the near-distance effect, the recorded raw intensity
(Iraw) value can be written as:
Where rd is the radius of the circular laser detector, d is the offset
between the measured range R and the object distance from the lens
plane, D is the diameter of the lens, Sd is the fixed distance of the
detector from the lens and f is the focal length. All of which are
parameters of the laser scanner. Combining Eq. (9) with Eq. (8) and
taking into account the near-distance effect, the recorded raw intensity
(Iraw) value can be written as:
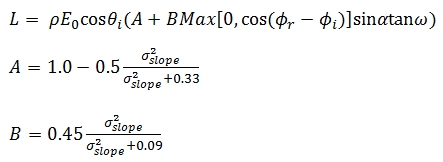 Where L is the radiance, E0 is the radiant flux received at normal
incidence angle in radians, ρ is the material reflectivity, α is the
incoming and ω the outgoing incidence angle, ϕr and ϕi are the reflected
and incident viewing azimuth angle in radians and σslope as the standard
deviation of the slope angle distribution in radians.
According to Carrea et al. (2016), the model Eq. (11) can be applied in
TLS systems where in terms of the configuration, the incidence and
reflected rays are coincident as expressed below:
Where L is the radiance, E0 is the radiant flux received at normal
incidence angle in radians, ρ is the material reflectivity, α is the
incoming and ω the outgoing incidence angle, ϕr and ϕi are the reflected
and incident viewing azimuth angle in radians and σslope as the standard
deviation of the slope angle distribution in radians.
According to Carrea et al. (2016), the model Eq. (11) can be applied in
TLS systems where in terms of the configuration, the incidence and
reflected rays are coincident as expressed below:
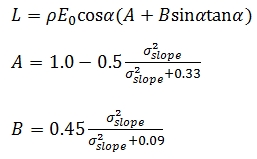 3.2.3 Hybrid Intensity
Correction Model
Since Eq. (10) has K as a constant, it can be simplified and rewritten
as:
3.2.3 Hybrid Intensity
Correction Model
Since Eq. (10) has K as a constant, it can be simplified and rewritten
as:
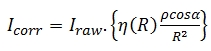 This intensity correction (Eq. (15)) can be used for perfect diffuse
scattering surfaces. However, for surfaces with micro-facets this
correction would not work well and so there is need to integrate the
standard deviation of the slope angle since each facet on the surface
has its own normal. Thus a hybrid intensity correction model that
considers near distance effects and also integrates the Oren-Nayar model
is proposed to improve the intensity correction.
This intensity correction (Eq. (15)) can be used for perfect diffuse
scattering surfaces. However, for surfaces with micro-facets this
correction would not work well and so there is need to integrate the
standard deviation of the slope angle since each facet on the surface
has its own normal. Thus a hybrid intensity correction model that
considers near distance effects and also integrates the Oren-Nayar model
is proposed to improve the intensity correction.
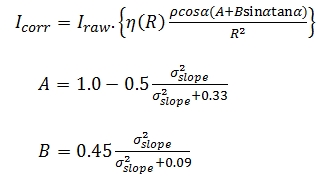 The standard deviation of the slope angle of facets (σslope) was
determined as in Carrea et al. (2016) and the following is an
explanation of the procedure. To obtain the optimal value for the slope
standard deviation (σslope), standardisation with respect to values
close to normal incidence was computed by using a sub-sample of points
that covered the area of the concrete block so as to reduce
computational intensity. Since the concrete blocks were fairly rough and
several points were scanned on the face on the block, it implies that
each point had its own incidence angle dependent on where the laser hit
on the block and the orientation of the normal at that position. This
being the case, an optimisation function was employed in order to
calculate the optimal value of σslope. Therefore, after the intensity
was corrected for near distance effects, it was then vital to compute
the optimal σslope value which would give a minimal variation of the
corrected intensity by taking into consideration the different incidence
angles. The optimisation function minimises the differences between the
mean corrected intensity values for the two intervals of the incidence
angle i.e. 0° to 10° and 0° to 45° by way of minimising to a single
variable on a fixed interval and so making it possible to obtain the
minimum of fσslope on a bounded interval [0, 1] as
written in Eq. (17) below:
The standard deviation of the slope angle of facets (σslope) was
determined as in Carrea et al. (2016) and the following is an
explanation of the procedure. To obtain the optimal value for the slope
standard deviation (σslope), standardisation with respect to values
close to normal incidence was computed by using a sub-sample of points
that covered the area of the concrete block so as to reduce
computational intensity. Since the concrete blocks were fairly rough and
several points were scanned on the face on the block, it implies that
each point had its own incidence angle dependent on where the laser hit
on the block and the orientation of the normal at that position. This
being the case, an optimisation function was employed in order to
calculate the optimal value of σslope. Therefore, after the intensity
was corrected for near distance effects, it was then vital to compute
the optimal σslope value which would give a minimal variation of the
corrected intensity by taking into consideration the different incidence
angles. The optimisation function minimises the differences between the
mean corrected intensity values for the two intervals of the incidence
angle i.e. 0° to 10° and 0° to 45° by way of minimising to a single
variable on a fixed interval and so making it possible to obtain the
minimum of fσslope on a bounded interval [0, 1] as
written in Eq. (17) below:
 The data processing and intensity correction method was implemented in
Matlab routines. The intensity value is dimensionless and for each
block, statistics such as intensity mean and standard deviation were
calculated. The average roughness (σslope) values for the blocks were
not so far away from 0° as values ranged from 1.15° to 2.58°. Concrete
reflectivity measurements were not taken due to non-availability of the
spectrometer which would measure reflectivity at a wavelength of 1500 nm
(which is the wavelength of the HDS7000 laser scanner used in this
study). However, we searched for documentation with concrete
reflectivity information at the desired wavelength and information was
found in Larsson et al. (2010). Based on this finding, the reflectance
of concrete is in the range between 0.300 to 0.400 (Fig. 4) and since
the concrete which was used in the study was gray and with some
roughness, it was a trial and error of reflectance values from 0.370 to
0.400.
The data processing and intensity correction method was implemented in
Matlab routines. The intensity value is dimensionless and for each
block, statistics such as intensity mean and standard deviation were
calculated. The average roughness (σslope) values for the blocks were
not so far away from 0° as values ranged from 1.15° to 2.58°. Concrete
reflectivity measurements were not taken due to non-availability of the
spectrometer which would measure reflectivity at a wavelength of 1500 nm
(which is the wavelength of the HDS7000 laser scanner used in this
study). However, we searched for documentation with concrete
reflectivity information at the desired wavelength and information was
found in Larsson et al. (2010). Based on this finding, the reflectance
of concrete is in the range between 0.300 to 0.400 (Fig. 4) and since
the concrete which was used in the study was gray and with some
roughness, it was a trial and error of reflectance values from 0.370 to
0.400. 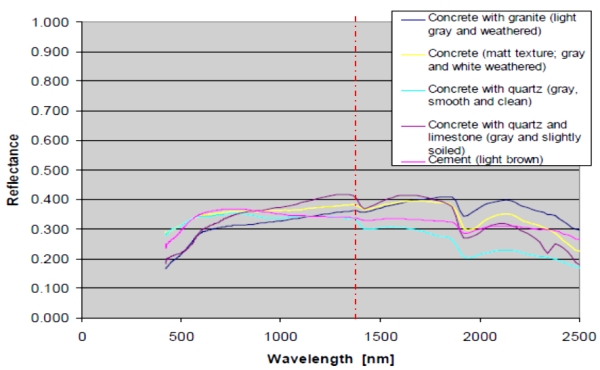 Fig. 4: Reflectivity spectrum of concrete and cement (Larsson et al., 2010) 4. RESULTS AND ANALYSIS 4.1 Intensity Standard Deviation and Distribution of Data The data acquired was analyzed to study for each block the relation between intensity standard deviation and intensity mean as was scanned at the five various incidence angles labelled A to E (see measurement setup in Fig. 3) and results are as shown in Fig. 5 below.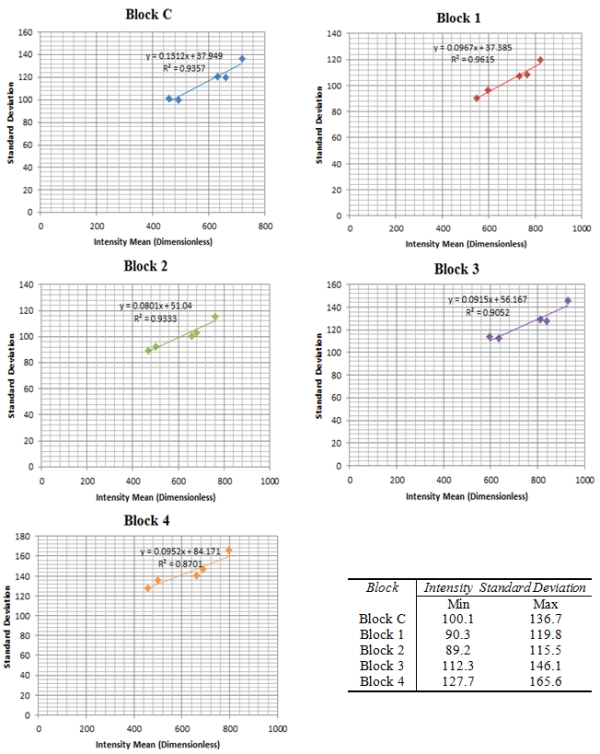 Fig. 5: Intensity standard deviation against intensity. Apparently, the standard deviation grows with the intensity mean for each block and this is verified in Fig. 5. Regardless of the scanning incidence angles which were 45°, 25°, 0°, -25° and -45°, the strength of the linear relationship between the two variables in Fig. 5 is strong as can be seen by the values of the coefficient of determination for each block. The minimal variation of the coefficient of determination of the blocks is due to the fact that their surfaces were not totally homogenous because the concrete aggregate cannot be uniformly distributed in all blocks although the same mix design was used. The distribution of the intensity data for the blocks scanned at various incidence angles was as assessed and taking Block C as an example, the results are as shown in Fig. 6.Fig. 6: Intensity data distribution at various incidence angles With reference to Fig. 6, two statistical parameters i.e. intensity mean and standard deviations were further investigated in exploratory data analysis of the intensity return at the various incidence angles. The data is normally distributed in all cases and as expected. In terms of the frequency, although the maximum count of 1800 was achievable at all incidence angles, the overall maximum mean intensity return was higher at normal angle of incidence where the point density is also high due to the nature of static TLS. Furthermore, as already pointed out in Fig. 5, the standard deviation grows with the intensity mean in Fig. 6. 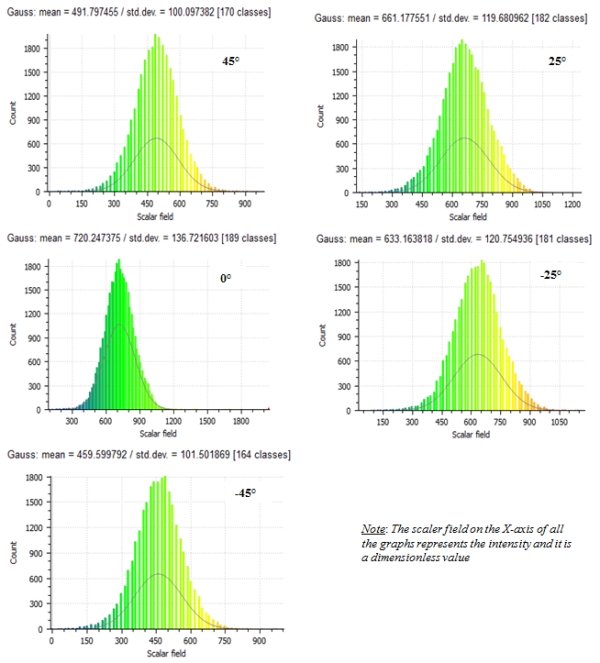
Fig. 6: Intensity data distribution at various incidence angles 4.2 Intensity and Incidence Angle (Before Correction) The blocks were scanned at various incidence angles with the distance at each scanning station held fixed. Fig. 7 and 8 show the resultant relationship between uncorrected intensity for all the blocks and the scanning angle of incidence.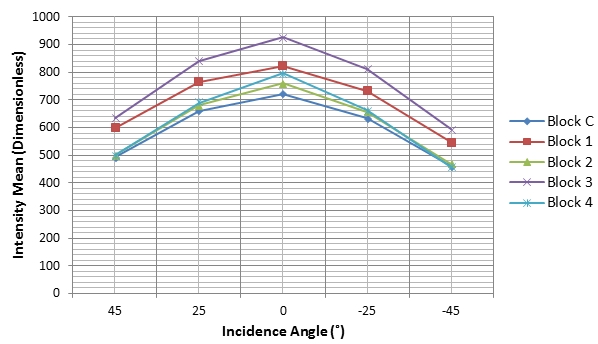 Fig. 7: Uncorrected intensity against incidence angle 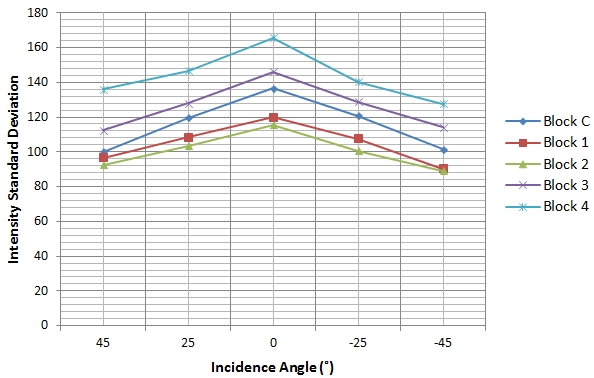 Fig. 8: Uncorrected intensity standard deviation against incidence angle The incidence angle effect in both Fig. 7 and 8 is visible and all blocks show the trend where the intensity decreases as the incidence angle increases and this is true theoretically, based on the radar range equation. As reported in theory, it can be seen that the closer the laser beam incidence angle is to 0° the more the returned intensity. Generally, higher incidence angles lead to a reduction in the amount of returned intensity and this becomes more pronounced when incidence angles are greater than 20° (Krooks et al., 2013) and for a Lambertian reflecting surface, the returned intensity has been predicted to decrease with the cosine of the incidence angle in accordance with Lambert’s cosine law (Eq. (18)):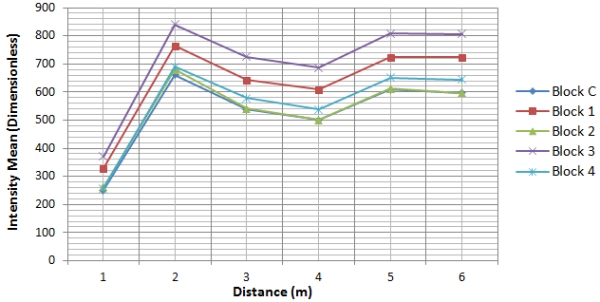 Fig. 9: Uncorrected intensity against distance The distance effects on the intensity can be seen since in theory, the returned intensity is expected to decrease with an increase in distance. The plausible reason for the unexpected results was atributed to the instrumental effects at short scanning distances and such results have also been reported by other researchers (e.g. Kaasalainen et al., 2011) although different scanners were used. Furthermore, in the same vein, Höfle (2014) states that past studies on TLS radiometric correction have clearly shown that the range dependence of TLS amplitude and intensity does not entirely follow the 1/R2 law of the radar equation as mostly valid for ALS, in particular at near distance of for instance less than 15 m. The reasons can be detector effects (e.g., brightness reducer, amplification, and gain control or receiver optics (defocusing and incomplete overlap of beam and receiver field of view). However, most manufacturers do not provide enough insight into developing a model-driven correction of these effects. 4.4 Intensity and Cosine Law Prediction vis-à-vis Incidence Angle The theoretical contribution of the incidence angle to the deterioration of the returned intensity is plotted in Fig. 10 and it follows Eq. (18). The function 1/cos(α) was also applied and it gave the same result in Fig. 10 and according to Yan and Shaker (2014), this is why the cosine of the incidence angle is commonly taken to be indirectly proportional to the corrected intensity (or spectral reflectance) in the correction process.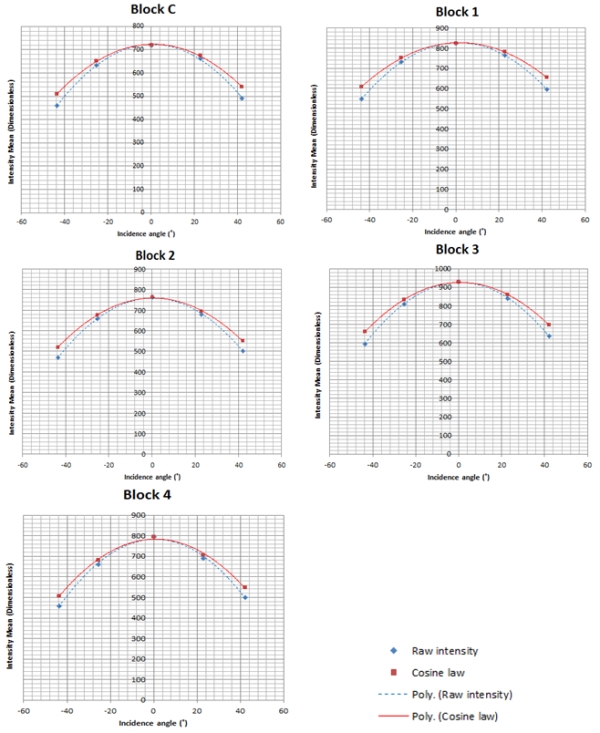 Fig. 10: Raw intensity and cosine law against incidence angle The relationship between the intensity and the incidence angle as well as Lambert’s cosine law is shown in Fig. 10. A close correlation between the raw intensity and that with the cosine law is evident though a constant and an offset of the cosine of the incidence angle may have to be added for more accurate results as suggested in Kaasalainen et al. (2011). However, Lambert’s cosine law still provides a good approximation of the incidence angle effects, especially up to about 20° of incidence (Kaasalainen et al., 2009b). Lambert’s cosine law can provide a satisfactory estimation of light absorption modelling for rough surfaces in both active and near-infrared spectral domains, thus, it is widely employed in existing intensity correction applications. However, Lambert’s cosine law is insufficient to correct the incidence angle effect for surfaces with increasing irregularity because these surfaces do not exactly follow the Lambertian scattering law. The incidence angle is related to target scattering properties, surface structure and scanning geometry. The interpretation of the incidence angle effect in terms of target surface properties is a complicated task (Tan and Cheng, 2016). However, Lambert’s cosine law has been successfully applied in some studies to correct the intensity for incidence angle effects. For instance, in Pfeifer et al. (2007) an experiment is reported with an Optech ILRIS3D laser scanner, where one target with near Lambertian scattering characteristics scanned at a distance close to 7m was observed at different angles. The intensity was corrected using the cosine correction and a linear amplification model. To visualize the effect of the cosine law on the intensity values in overall scale, the average difference between the raw and cosine predicted intensity data points was plotted as shown in Fig. 11(a) for Block C as an example. Fig. 11(b) shows the raw intensity of Block C and the error bars indicate the average standard deviation.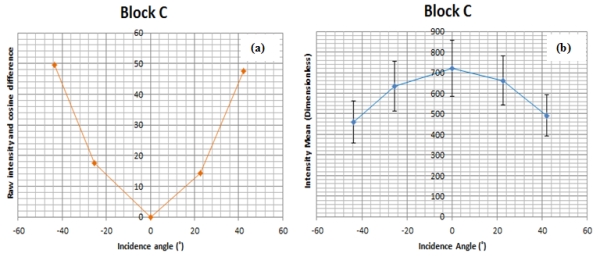 Fig. 11: Difference between raw intensity and cosine law against incidence angle Compared to the error range of the intensity for Block C in Fig. 11(b), the difference between the raw intensity and that with the cosine law is still quite minimal, which in percentage terms ranges from 0% at normal incidence angle to about 11% at 45°. This means that the accuracy of the cosine law is sufficient to predict the reflectance at this level of accuracy but may have limitations at higher angles of incidence as already pointed out above. However, the improved intensity correction method did not relay on the cosine law for incidence angle correction since it is insufficient to consider target surface characteristics, and more so its limitations beyond 20° of incidence angle. 4.5 Improved Intensity Correction Method The procedural steps for the improved intensity correction method involve, first correcting intensity data for near-distance effects which are evident in Fig. 9 by applying the near-distance correction method presented above and after that the incidence angle and distance effects on the intensity can be solved separately since they do not mix. According to Fang et al. (2015), in a study where the Z+F Imager 5006i laser scanner was used, the parameters in Eq. (9) have a physical basis and that the derived parameters in Table 2 were estimated in accordance with observed values such as the receiver’s diameter and the detector’s distance from the lens plane by iterative curve fitting using a nonlinear least squares method and robust Gauss-Newton algorithm. However, the values of the parameters differ for the various laser scanners and so each laser scanner needs to be studied.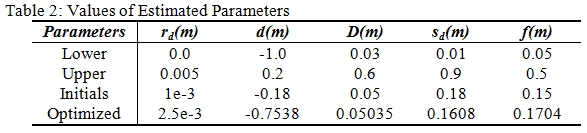 Although the estimated parameters in Table 2 were obtained using the Z+F
Imager 5006i laser scanner, the parameters were tested for the HDS7000
laser scanner with success since the two instruments are coaxial and
basically identical in terms of their physical characteristics as
designed by the manufacturer. Fig. 12 below shows the results after
applying the near-distance correction and it can be seen that the
correction is valid for distances from 2m and greater since all the
other scanning distances investigated follow the theoretical range
squared inverse law in relation to the returned intensity and the
measured distances. As already alluded to above, instrumental effects
such as near-distance reducers (which are meant to avoid over-exposure
of the sensor) are known to have an influence on the returned intensity
and this actually makes the laser range equation to be inapplicable at
all distances as a physical model for intensity correction.
Although the estimated parameters in Table 2 were obtained using the Z+F
Imager 5006i laser scanner, the parameters were tested for the HDS7000
laser scanner with success since the two instruments are coaxial and
basically identical in terms of their physical characteristics as
designed by the manufacturer. Fig. 12 below shows the results after
applying the near-distance correction and it can be seen that the
correction is valid for distances from 2m and greater since all the
other scanning distances investigated follow the theoretical range
squared inverse law in relation to the returned intensity and the
measured distances. As already alluded to above, instrumental effects
such as near-distance reducers (which are meant to avoid over-exposure
of the sensor) are known to have an influence on the returned intensity
and this actually makes the laser range equation to be inapplicable at
all distances as a physical model for intensity correction.
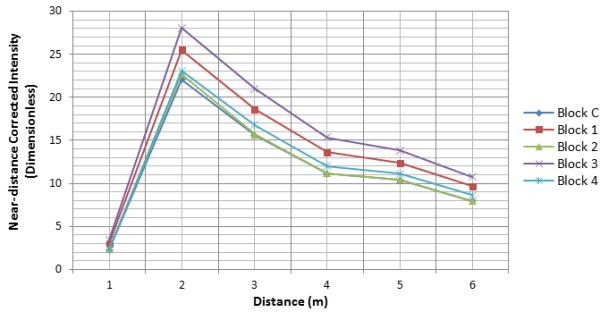 Fig. 12: Near-distance corrected intensity against distance 4.5.1 Intensity and Distance (After Correction) Fig. 13 below shows the results of the relationship of intensity against distance after applying correction on the intensity data. With the exception of 1m, the correction is valid from 2m and all the other distances that the concrete was scanned from.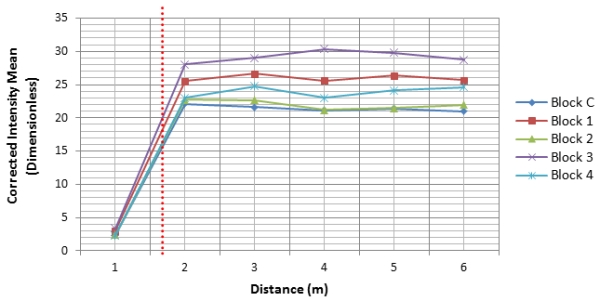 Fig. 13: Corrected intensity against Distance 4.5.2 Intensity and Incidence Angle (After Correction) The relationship of the corrected intensity against incidence angle is as shown in Fig. 14. It can be observed that for all the angles of incidence that were investigated, the intensity correction method is valid. The incidence angle effect on the intensity decreased as the graphs for all the blocks tend to straighten cross the whole range of the incidence angles.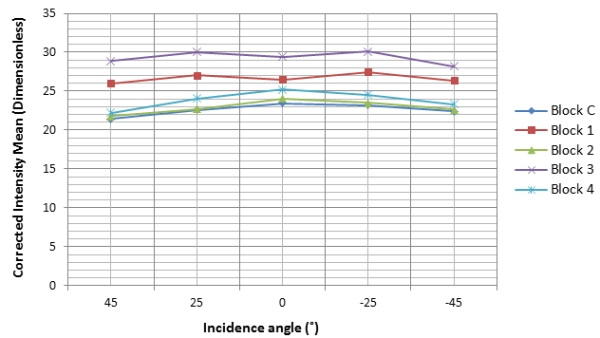 Fig. 14: Corrected intensity against incidence angle Although the incidence angle effects appear to have significantly reduced in Fig. 14, the dominance of the reflectance for each block on the incidence angle behaviour can be seen and this could be because the blocks were not completely the same. 5. DISCUSSION AND CONCLUSION The effects of the distance and incidence angle on the intensity of concrete specimens have been analysed by looking at the relationship of each with the intensity and they were found to be independent as also reported by some past researchers and this makes it possible to correct both by using different models that are independent of the measurement. Results of the uncorrected intensity and distance relationship have shown that intensity measurements from the HDS7000 scanner at near distances have instrumental effects and several other researchers as mentioned in the reviewed material have reported a similar finding even though different types scanners were used. The distance and incidence angle effects for the HDS7000 concrete intensity data were corrected using the improved method and this method has shown the potential to correct the intensity at scanning distances from 2m and greater. The correction of intensity for near distance effects is important for studies that require measurements to be taken at shorter baselines. The raw intensity in relation to that with the cosine law prediction did show a close relationship indicating that the cosine law provides a good approximation of the incidence angle effects and the more reason it is used in intensity correction schemes. However, Reshetyuk (2006) observed that the intensity return decreased with an increase in angle of incidence through experiments carried out using the HDS3000 scanner although the scanned target (a wall) was not Lambertian. It has been reported in some studies that even when the raw intensity may appear to follow the cosine law prediction, there is no guarantee that the Lambert’s cosine law would correct the intensity data for incidence angle effects as for instance pointed out in Tan and Cheng (2016) where a FARO Focus3D 120 scanner was used and a differerent intensity correction method was actually applied. Furthermore, they have stated that the incidence angle is related to target scattering properties, surface structure and scanning geometry and that the interpretation of the incidence angle effect in terms of target surface properties is a complicated task. Surface roughness of the scanned target is also a factor that can influence the returned intensity and the concrete that was used in this study had roughness ranging from millimeters to a few centimeters. Athough the magnitude of concrete roughness may seem to be small, it had an influence though minimal on the intensity correction. An improved intensity correction method such as the one presented could be potentially beneficial in several applications such as change detection, material classification and segmentation. The following conclusions have been drawn from this study and in relation to the wider context of the subject in past research work:
The University of Nottingham, Ningbo, China. Faculty of Science and Engineering Department of Civil Engineering 199 Taikang East Road Ningbo 315100 CHINA Email: wallace.mukupa@nottingham.edu.cn
|